De vegades no podem evitar cert grau d’incertesa a l’hora d’estudiar un fenomen, però mentre en siguem conscients no cal menysprear cap dada.
Heu jugat ja al joc interactiu de les granotes? És un dels 4 jocs interactius que ha desenvolupat el Museu de Matemàtiques de Catalunya (MMACA) a Recerca en Acció amb el finançament de la Fecyt.
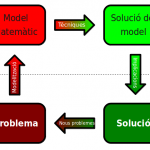
Fins ara hem vist exemples de models que ens permetien obtenir respostes precises a les nostres preguntes. Quants moviments calen per resoldre les Torres de Hanoi i quins són? Quines habitacions del Laberint podem eliminar i quines no?…
De vegades, però, no disposem d’un model matemàtic prou complet per a predir completament un fenomen o no disposem de les eines per resoldre’l. Fins no fa gaire, sense anar més lluny, els científics no podien comptar amb l’ajut dels ordinadors per fer els extensos càlculs que requereixen alguns models i van haver d’inventar alternatives.
Un dels trucs més habituals va ser fer ús de l’estadística per estudiar fenòmens que tradicionalment no hi havien tingut cap relació. Cadenes de Markov, combinatòria, teoria de cues… molts dels models que els científics fan servir a l’actualitat encara incorporen aquests elements. Avui veurem un exemple senzill.
Anem a pescar al riu!
El joc de les Granotes et sorprèn quan hi jugues per primera vegada i et torna a sorprendre quan entens com funciona.
El primer que trobes és una granota que et demana que triïs una pedra a l’atzar i saltis, de pedra en pedra, al llarg del riu. Quan arribes al final, la granota, que no sap quina pedra has triat en primer lloc, és capaç d’endevinar a quina pedra has acabat el teu camí. Sorprès? Doncs el millor està per arribar.
Qualsevol podria pensar que el que fa l’ordinador és calcular ràpidament tots els camins possibles i escollir aquell que considera més probable o bé que psicòlegs experts en prestidigitació ens han informat quines són les cartes que la gent acostuma a triar més sovint. De fet totes dues coses segurament haurien funcionat, però no cal fer-les. El joc de les granotes és encara més senzill.
Resulta que fent servir models estocàstics (que són aquells que incorporen variables aleatòries) podem adonar-nos que tots els camins conduiran, gairebé sempre, a la mateixa pedra. L’ordinador no necessita calcular tots els camins, només li cal calcular-ne un, a l’atzar, i encertarà gairebé sempre!
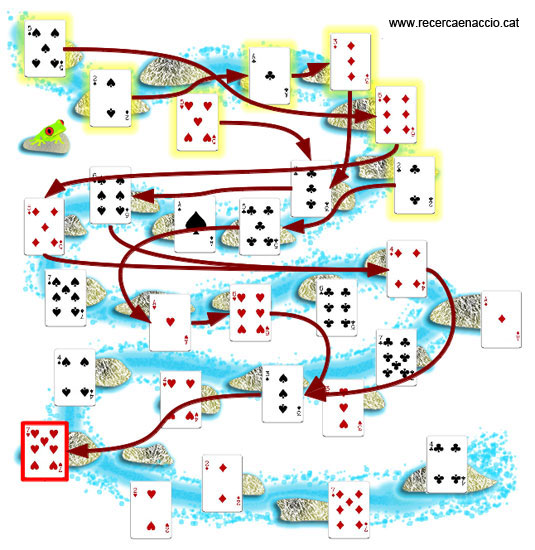
El joc de les granotes amb els salts dibuixats.
Com podeu veure a la imatge, dos camins que passin per una mateixa pedra aniran junts fins al final del joc. Així, a poc a poc, els camins s’aniran ajuntant per pur atzar i, quan arribem al final del riu, ja només en quedarà un.
Cal, però, tenir cura. És possible que, situant les cartes a l’atzar, el riu s’acabi abans que els camins convergeixin del tot i, en aquests casos, la granota es pot equivocar.
Noves idees, nous reptes
La feina d’un científic no s’acaba aquí. El model que tenim es pot millorar fent servir eines més potents o incloent-hi altres factors. Podríem, per exemple, calcular tots els possibles camins i agafar el que contingui més “fusions”, aprofitant que els ordinadors d’avui dia són molt potents, o podríem incorporar la psicologia en comptes de suposar que l’espectador decidirà a l’atzar…
Se t’acudeixen més idees per millorar el nostre programa?
MMACA, Museu de Matemàtiques de Catalunya
Fins ara hem vist exemples de models que ens permetien obtenir respostes precises a les nostres preguntes. Quants moviments calen per resoldre les Torres de Hanoi i quins són? Quines habitacions del Laberint podem eliminar i quines no?…
De vegades, però, no disposem d’un model matemàtic prou complet per a predir completament un fenomen o no disposem de les eines per resoldre’l. Fins no fa gaire, sense anar més lluny, els científics no podien comptar amb l’ajut dels ordinadors per fer els extensos càlculs que requereixen alguns models i van haver d’inventar alternatives.
Un dels trucs més habituals va ser fer ús de l’estadística per estudiar fenòmens que tradicionalment no hi havien tingut cap relació. Cadenes de Markov, combinatòria, teoria de cues… molts dels models que els científics fan servir a l’actualitat encara incorporen aquests elements. Avui veurem un exemple senzill.
Anem a pescar al riu!
El joc de les Granotes et sorprèn quan hi jugues per primera vegada i et torna a sorprendre quan entens com funciona.
El primer que trobes és una granota que et demana que triïs una pedra a l’atzar i saltis, de pedra en pedra, al llarg del riu. Quan arribes al final, la granota, que no sap quina pedra has triat en primer lloc, és capaç d’endevinar a quina pedra has acabat el teu camí. Sorprès? Doncs el millor està per arribar.
Qualsevol podria pensar que el que fa l’ordinador és calcular ràpidament tots els camins possibles i escollir aquell que considera més probable o bé que psicòlegs experts en prestidigitació ens han informat quines són les cartes que la gent acostuma a triar més sovint. De fet totes dues coses segurament haurien funcionat, però no cal fer-les. El joc de les granotes és encara més senzill.
Resulta que fent servir models estocàstics (que són aquells que incorporen variables aleatòries) podem adonar-nos que tots els camins conduiran, gairebé sempre, a la mateixa pedra. L’ordinador no necessita calcular tots els camins, només li cal calcular-ne un, a l’atzar, i encertarà gairebé sempre!

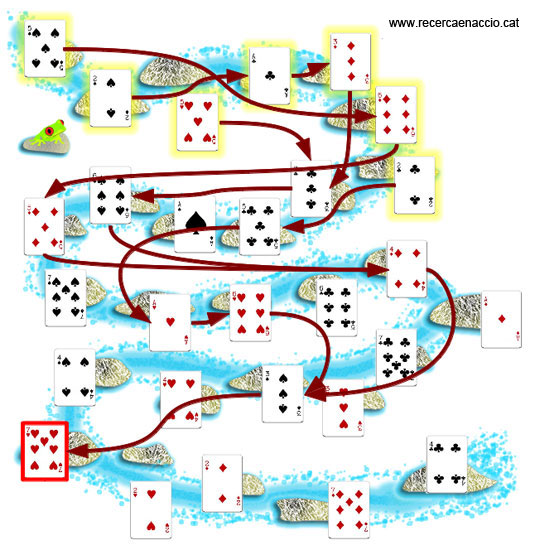
El joc de les granotes amb els salts dibuixats.
Com podeu veure a la imatge, dos camins que passin per una mateixa pedra aniran junts fins al final del joc. Així, a poc a poc, els camins s’aniran ajuntant per pur atzar i, quan arribem al final del riu, ja només en quedarà un.
Cal, però, tenir cura. És possible que, situant les cartes a l’atzar, el riu s’acabi abans que els camins convergeixin del tot i, en aquests casos, la granota es pot equivocar.
Noves idees, nous reptes
La feina d’un científic no s’acaba aquí. El model que tenim es pot millorar fent servir eines més potents o incloent-hi altres factors. Podríem, per exemple, calcular tots els possibles camins i agafar el que contingui més “fusions”, aprofitant que els ordinadors d’avui dia són molt potents, o podríem incorporar la psicologia en comptes de suposar que l’espectador decidirà a l’atzar…
Se t’acudeixen més idees per millorar el nostre programa?
MMACA, Museu de Matemàtiques de Catalunya














0 Comentaris