A partir d’aquest missatge, però, ha arribat l’hora d’aprofundir en exemples reals d’investigació científica. Parlarem amb investigadors de grups de recerca catalans que, d’una manera o altra, facin servir la modelització matemàtica als seus estudis de física, química, enginyeria, sociologia, etc.
Abans, però, hem d’aprendre algunes coses sobre la modelització, com ara quines parts té i què s’ha de tenir en compte en cada pas. Si ens acompanyeu les properes setmanes podreu aprendre com es fa un bon model matemàtic i, fins i tot, començar a fer els vostres propis models del món que us envolta!
Houston… tenim un problema!
Cada cop que un científic vol estudiar un fenomen de la natura, cada cop que un enginyer vol fer servir la tecnologia per resoldre un problema, cada cop que un sociòleg vol comprendre millor el comportament d’un determinat grup… necessiten un model matemàtic.
Aquests models ens permeten resoldre problemes fent servir eines matemàtiques i computacionals i ens ajuden a simular la realitat per poder preveure les conseqüències dels nostres actes (com ara el resultat d’una reacció química o la introducció d’una nova llei) sense por de patir conseqüències no desitjades.
Així doncs, podríem dir, que la feina de tot científic consisteix a adonar-se que hi ha un problema, imaginar una possible solució i cercar el camí que uneix un i l’altra.

Plantejament d’un projecte científic.
Així, un possible problema seria “volem saber com es propaga certa malaltia” i el tipus de solució que busquem serà informació respecte a quins mitjans afavoreixen i quins mitjans alenteixen la propagació de la malaltia.
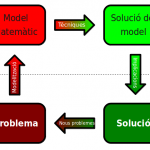
La modelització matemàtica entra en joc quan ja tenim definits el problema i el tipus de solució que volem trobar i ens permet passar d’un problema real, amb milers de detalls i peculiaritats que ens poden distreure, a un problema abstracte, idealitzat, que es pot atacar fent servir eines matemàtiques.
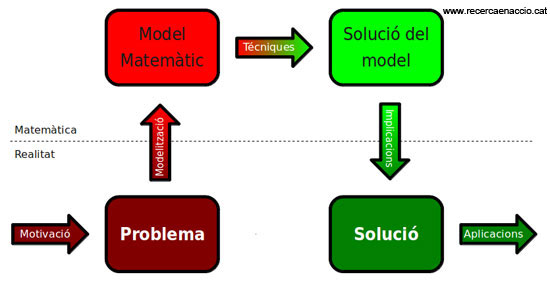
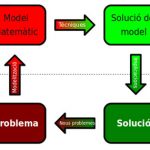
Procés de resolució d’un problema mitjançant la modelització matemàtica.
Un bon model
Així, un cop tenim clar quin problema volem resoldre i quin tipus de resposta volem obtenir el que cal és buscar un bon model matemàtic que ens permeti manipular les nostres dades i extreure’n respostes concretes.
Però models n’hi ha molts, fins i tot si només ens fixem en aquells que proporcionen el tipus de resposta que volem obtenir. Així, caldrà disposar d’una sèrie de criteris per tal de triar-ne el millor:
- És correcte el nostre model? Si el model no reflecteix els processos i els resultats del fenomen que estem estudiant no ens servirà de gaire… Per exemple, en el cas de la malaltia no tindria sentit un model que digués que la malaltia és més present a les zones on no viu ningú i desapareix a les zones molt poblades perquè saben que això no és cert.
- És prou precís el nostre model? Si el model és correcte, però les dades que n’obtenim no resulten prou fiables no podrem aplicar les solucions obtingudes a la vida real. Si volem saber a quin ritme es propagarà la malaltia i quines ciutats es veuran afectades abans, un model que només ens indiqui quins països patiran abans la malaltia no ens és útil. Resulta una resposta poc precisa.
- Podem resoldre el model? Fins i tot si el nostre model és correcte i prou precís cal que puguem resoldre’l amb les eines matemàtiques i computacionals que tenim a l’abast. Sovint és bona idea deixar fora del model els detalls menys importants. Si no som capaços de resoldre les equacions que resulten del nostre model o si un ordinador triga més a predir on arribarà la malaltia que el que triga la malaltia a arribar-hi… estem fent tard!
Com veieu, els científics han de tenir en compte molts factors i han de disposar d’amplis coneixements per fer bé aquesta part de la feina… i només és el primer pas!
I ara què?
Un cop tenim un bon model matemàtic del fenomen que volem estudiar és hora de resoldre’l i d’interpretar les respostes obtingudes. Com veurem, sovint hi ha més d’una manera de resoldre un mateix model i la interpretació de les respostes no sempre és directa i evident… Però això serà tema de conversa per a un altre missatge. Per avui ja hi ha hagut prou teoria!
MMACA, Museu de Matemàtiques de Catalunya















Clar i català
Un molt bon inici de modelització
A veure les propostes
Felicitats